表計算ソフトによる曲線あてはめ作業

2015-08-30 公開、 2020-03-21 更新

概要

　ExcelやLibreOffice Calc、Google スプレッドシートなどの表計算ソフトを使用した曲線あてはめによるデータ補間のやり方について紹介します。当記事は、分子に変数を含まない一次分数関数や二次分数関数への曲線あてはめ手法解説を特色としています。

　具体的な曲線あてはめの手段としては、グラフを作成してから近似曲線とその式を表示させてラベルから近似曲線の式の係数を得る手法と、表計算ソフトの関数から直接係数もしくは近似曲線のY座標値を得る二種類の手法があります。なお、この記事で説明する事柄において、「曲線」には一次関数による「直線」も含まれていることに留意してください。

　当記事の解説の実例を示したサンプルシートを以下にて公開します。解説とあわせてご覧ください。

>>Download xlsx file (curve-fitting-sample.xlsx)

>>Download xls file (curve-fitting-sample.xls) - Excel2003以前向け

曲線あてはめとは

　曲線あてはめについて簡単に説明します。専門家ではないため、正確に説明できているかの保証は致しかねます。参考程度にご覧ください。

　まず、ある座標データのセットをあらわすのにふさわしいと考えられる関数を選定します（例：直巻モータのトルクは理論的には電流の二乗に比例するため、そのトルク特性データには二次関数を適用）。次に、選定した関数の曲線がそのデータセットに最もあてはまるよう、関数の各係数を求めます。係数を求める手法として代表的なものは最小二乗法が挙げられます。最小二乗法そのものは難解ですが、各種表計算アプリでは係数を座標データから直接求める手段が用意されており、実用上はその難解さを意識することはありません。こうして求められた関数の曲線を近似曲線と呼び、一般に各データの座標点を通りません。

　座標データから外れた箇所のデータを推定する手段としては別に「補間」がありますが、これはデータ全体に特定の数式をあてはめず、求めたい数値の近傍にある数個のデータから値を推定する点で曲線曲線あてはめとは異なります（例：線形補間では近傍の2点）。また、他データ推定曲線が元のデータ座標を通ることも、曲線あてはめと異なる点です。

グラフに示す近似曲線の式の利用

　散布図グラフを作成し、近似曲線をそこに追加することにより近似曲線の各係数を求めます。この手法は、ExcelやGoogle スプレッドシートで使用できます。直感的な作業であり取っつきやすいのがメリットですが、地味な手作業が多く、作業する曲線の数が多いと手間がかかるというデメリットがあります。表計算ソフトに慣れている方なら、後述のLINEST関数を利用した手法やTREND関数を使用した手法の利用を検討されることをおすすめします。

散布図グラフの作成

　近似曲線をあてはめたいデータを選択しグラフを作成します。グラフの種類は「散布図」を選択します。

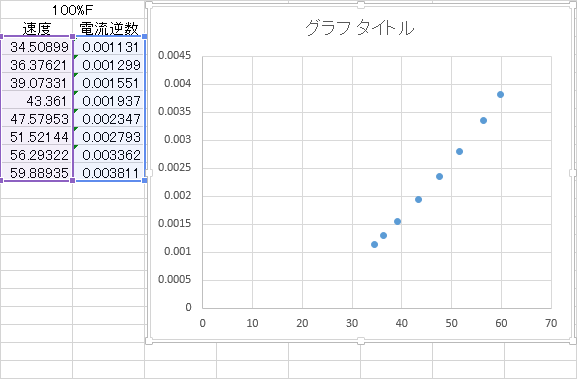
散布図グラフの作成（Excel）

近似曲線の追加と係数取得

Excelの場合

　プロットを右クリックして「近似曲線の追加(R)」を選択します。

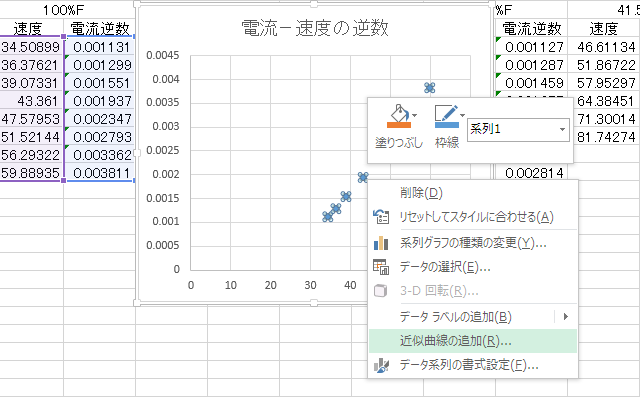
近似曲線の追加（Excel）

　次に近似曲線の書式設定を行います。二次関数もしくは二次分数関数の曲線をあてはめる場合、「多項式近似(P)」を選択し、「次数(D)」は「2」とします。一次関数（直線）の場合はそのままにします。「グラフに数式を表示する(E)」にチェックを入れることで、グラフ上に近似曲線の式が表示されます。

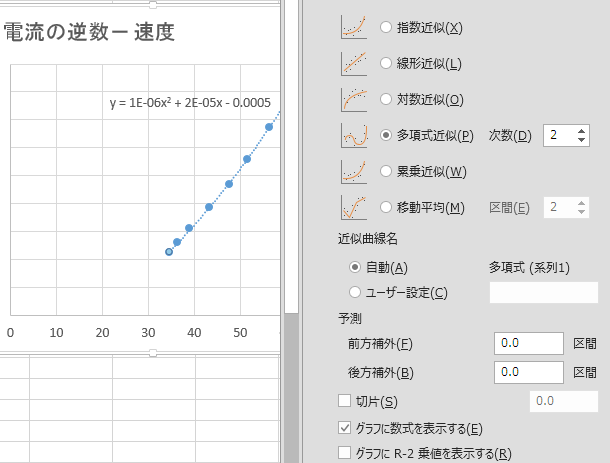
近似曲線の書式設定（Excel）

　表示された式から係数をコピーします。

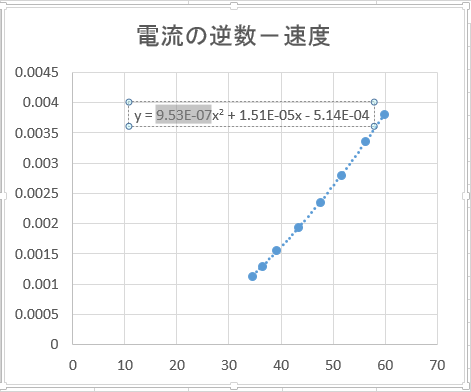
近似曲線の係数のコピー（Excel）

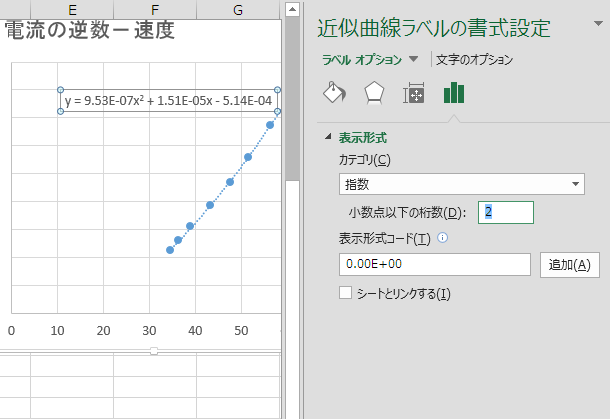
　なお、近似曲線の式ラベルの表示形式を「指数」に設定し、さらに「小数点以下の桁数(D)」を2~3程度にすれば、係数が極端に小さい場合においてより正確な係数が得られます。指数表示は有理数rと整数nにより「rEn」の形で表記され、実際の数値は「r * 10ⁿ」となります。例えば、1.23E+01は12.3、1.23E-01は0.123といった値を表しています。

近似曲線の式ラベルの表示形式変更（Excel）

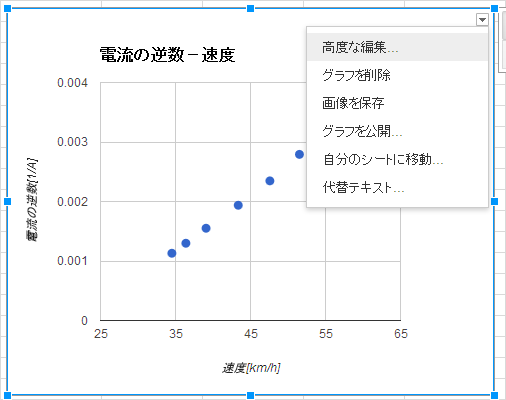
Google スプレッドシートの場合

　グラフの右上の編集メニューから「高度な編集...」を選択します。

Googleスプレッドシートのグラフ編集

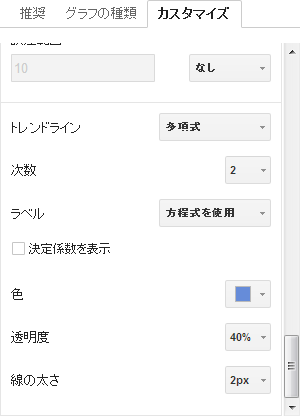
　「カスタマイズ」タブの一番下にある、「トレンドライン」の選択リストから「線形」（直線の場合）もしくは「多項式」（二次関数もしくは二次分数関数の曲線の場合）を選択します。後者の場合は、次数を2に設定します。また、「ラベル」は「方程式を使用」を選択します。

近似曲線の追加（Googleスプレッドシート）

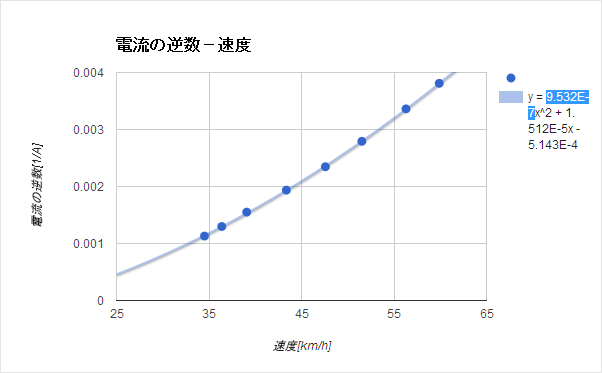
　右のプレビュー表示上に現れた式から係数をコピーします。凡例の文字列は通常はコピーすることができませんが、編集画面のプレビュー表示上では文字列を選択して「Ctrl + Vキー」を押すことでコピーすることができます。

近似曲線の係数のコピー（Googleスプレッドシート）

曲線のy座標を求める式の作成

　上記の関数にて求めた係数を用いて以下の式を作成し、曲線のy座標値を求めます。

関数	式
一次	=係数a*新規x+係数b
二次	=係数a新規x^2+係数bxの値+係数c
一次分数	=1/(係数a*新規x+係数b)
二次分数	=1/(係数a新規x^2+係数b新規x+係数c）

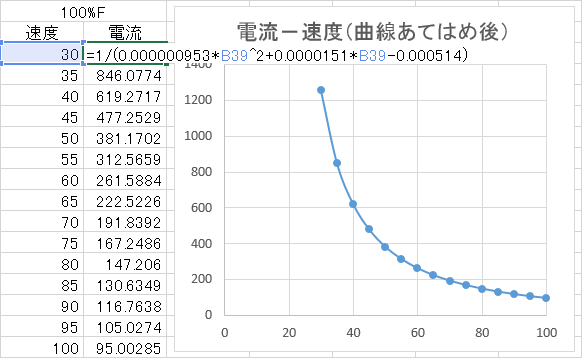
近似曲線のy座標値の計算

LINEST関数の利用

　表計算ソフトに実装されているLINEST関数などを利用することにより、データから直接近似曲線の式の係数を求め、得られた係数から曲線の式を作成し、最終的に規則的なx座標値を代入して曲線上のy座標値を求めます。少々取っつきにくいですが、表計算ソフトの取り扱いに習熟していれば手早く補間を行うことができます。Excel、Google スプレッドシート、LibreOffice Calcで動作を確認しています。

　LINEST関数の仕様については当解説では触れず、実際の利用方法を紹介するに留めます。詳細を知りたい方は、以下のページを参考にしてみてください。

技術計算製作所-/excel/numcal/regress:

　なお、以下に掲載する式は値の選択範囲に空白セルが含まれるとエラーが発生するため、そのままでは使い勝手が良くありません。実用性を持たせるためにはCOUNT関数とOFFSET関数を組み合わせ、既知xと既知ｙの選択範囲をデータ個数に合わせて可変にするなどの工夫を行う必要があります。COUNT関数とOFFSET関数を組み合わせた可変選択範囲の作り方はこちらでは省略します。既存の別サイトの解説をご覧ください。

係数を求める式の追加

　2つ以上の既知のxと既知のyの組にあてはめられる一次関数（直線）\[y = ax + b\]の各係数は、以下の式を使用することで得られます。SLOPE関数は直線の傾きを、INTERCEPTは切片を求める関数です。

係数	式
\(a\)	=SLOPE(既知y範囲,既知x範囲）
\(b\)	=INTERCEPT(既知y範囲,既知x範囲）

　3つ以上の既知のxと既知のyの組にあてはめられる二次関数\[y = ax^2 + bx + c\]の各係数は、以下の式を使用することで得られます。LINEST関数の出力は配列形式のため、INDEX関数で配列の個々の要素を取り出しています。

　以下の式のうち、中かっこ『{}』が含まれる式は配列数式です。ExcelやGoogleスプレッドシートではそのまま入力してもエラーにはなりませんが、LibreOffice Calcでは入力確定時にCtrl + Shift + Enterキーの同時押しを行い配列数式として明示的に入力しないとエラーになりますのでご注意ください。LibreOffice Calcでは配列数式のオートフィルが行えず、少々使い勝手が悪いです。

係数	式
\(a\)	=INDEX(LINEST(既知y範囲,既知x範囲^{1,2}),1,1）
\(b\)	=INDEX(LINEST(既知y範囲,既知x範囲^{1,2}),1,2）
\(c\)	=INDEX(LINEST(既知y範囲,既知x範囲^{1,2}),1,3）

　一次関数\[y = \frac{1}{ax + b}\]の各係数は、上に掲載した式を変形した以下の式を使用することで得られます。

係数	式
\(a\)	=SLOPE({1}/既知y範囲,既知x範囲）
\(b\)	=INTERCEPT({1}/既知y範囲,既知x範囲）

　また、二次分数関数\[y = \frac{1}{ax^2 + bx + c}\]の各係数は、以下の式を使用することで得られます。

係数	式
\(a\)	=INDEX(LINEST({1}/既知y範囲,既知x範囲^{1,2}),1,1）
\(b\)	=INDEX(LINEST({1}/既知y範囲,既知x範囲^{1,2}),1,2）
\(c\)	=INDEX(LINEST({1}/既知y範囲,既知x範囲^{1,2}),1,3）

曲線のy座標を求める式の作成

　上記の関数にて求めた係数を用いて以下の式を作成し、曲線のy座標値を求めます。

関数	式
一次	=係数a*新規x+係数b
二次	=係数a新規x^2+係数b新規x+係数c
一次分数	=1/(係数a*新規x+係数b）
二次分数	=1/(係数a新規x^2+係数b新規x+係数c）

TREND関数の利用

　TREND関数を利用すれば、作業用のセルを作る必要が無く単一の関数で近似曲線のy座標値を求めることができます。以下の式のうち、中カッコ『{}』の付いた式は先ほどと同様配列数式であり、Excelはそのまま入力可能ですが、LibreOffice CalcとGoogleスプレッドシートでは入力確定時にCtrl + Shift + Enterキーの同時押しを行い配列数式として明示的に入力しないとエラーになります。既知の値の選択範囲に空白セルが含まれるとエラーを起こすのもLINEST関数と同様であり、データ数がバラバラな複数の項目に対して汎用的に使用するためには、さらにCOUNT関数とOFFSET関数を組み合わせてTRAND関数に与えるデータ範囲を可変とするなど、一工夫する必要があります。

関数	式
一次	=TREND(既知y範囲,既知x範囲,新規x)
二次	=TREND(既知y範囲,既知x範囲^{1,2},新規x^{1,2})
一次分数	=1/TREND({1}/既知y範囲,既知x範囲,新規x)
二次分数	=1/TREND({1}/既知y範囲,既知x範囲^{1,2},新規x^{1,2})